Multiphase flow correlations

The primary purpose of a multiphase flow correlations is to predict the liquid holdup (and hence the flowing mixture density) and the frictional pressure gradient. This article details the most widely used correlations for the prediction of the Vertical Lift Performance.

The oil and water are lumped together as one equivalent fluid. Thus flow correlations in common use consider liquid/gas interactions. They are therefore more correctly termed two-phase flow correlations. Depending on the particular correlation, flow regimes are identified and specialized holdup and friction gradient calculations are applied for each flow regime.

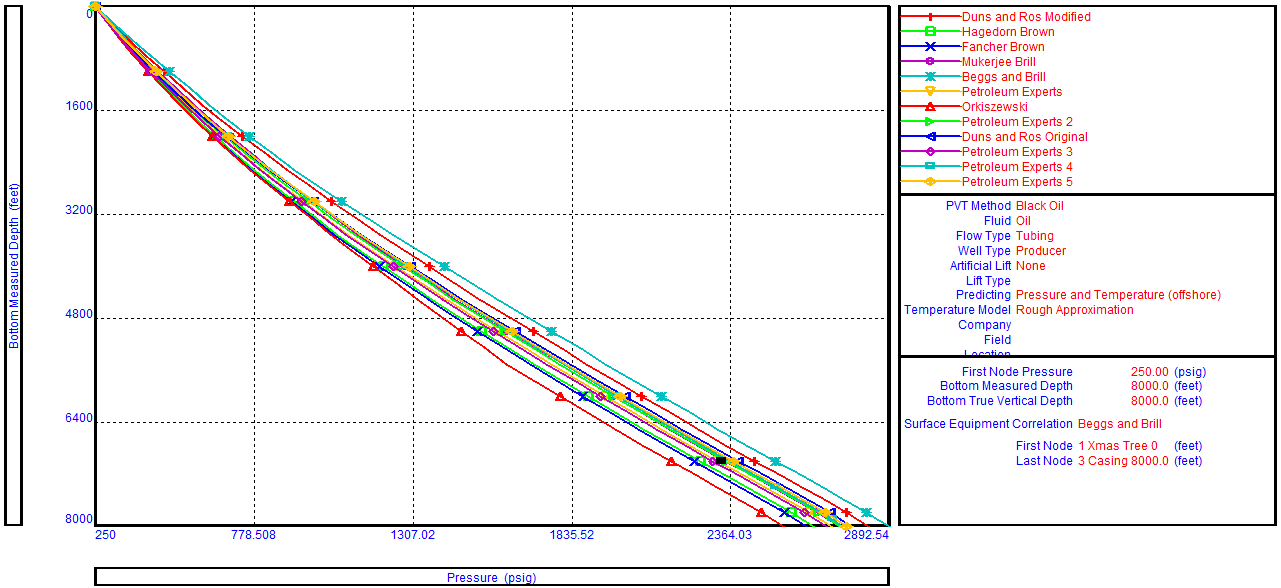
There is no universal rule for selecting the best flow correlation for a given application. When an outflow performance simulator is used, it is recommended that a Correlation Comparison always be carried out. By inspecting the predicted flow regimes and pressure results, the User can select the correlation that best models the physical situation.

Multiphase flow correlations:

Fancher & Brown:

Fancher and Brown is a no-slip correlation, with no flow regime map. Therefore, this correlation cannot be recommended for general use and it is provided for use as a quality control (should not be used for quantitative work).
It gives the lowest possible value of Vertical lift Performance (VLP). Therefore, Measured data falling to the left of Fancher Brown on the correlation comparison plot indicates a problem with fluid density (i.e PVT) or field pressure data.
According to Brown, it is only suitable for 2-3/8 – 2-7/8 inch tubing.
It is for GLR less than 5000 scf/bbl and flow rates less than 400 bpd.
It has its own friction factor model, which is independent of pipe roughness.

Duns and Ros (Std.):

The Duns & Ros correlation was developed for vertical flow of gas and liquid mixtures in wells.
The equations were based on extensive experimental work using oil and air mixtures.
Usually perform well for wells where high gas-liquid ratios (usually in mist flow regime) and condensate wells.

Duns and Ros (modified):

It has a flow regime map extended by the work of Gould et al. This includes a new transition region between bubble and slug flow, and an additional froth flow region at high flow rates. The holdup is considered as no-slip for froth flow, and is interpolated over the bubble-slug transition.
The other holdup relationships are as for the standard Duns and Ros. Friction is calculated by the method proposed by Kleyweg. This uses a monophasic friction factor rather than two-phase, but involves use of an average fluid velocity. This is claimed by Kleyweg to be a better method.
Duns and Ros Modified gives the highest pressure drops in the slug flow regime for oil wells.

Note: Fancher Brown (no slip) and Duns and Ros Modified can serve as quality check boundaries for downhole measurements.

Hagedorn & Brown:

It was the results of an experimental study of pressure gradients occurring during continuous two-phase flow in small diameter vertical conduits. Hagedorn and Brow have developed this correlation from 475 tests in a 1,500 foot experimental well using fluids with viscosities up to 110 centipoise and through 1 inch, 1¼ inch, and 1½ inch nominal size tubing.
There is no change to holdup with deviation. A two-phase friction factor using pipe roughness is used.
It is probably the most widely applied of all oil well VLP correlations. It works well for bubble and slug flow regimes in a wide range of applications. It performs well in oil wells for slug flow at moderate to high production rates
It under predicts VLP at low rates (well loading is poorly predicted) and should not be used for predicting minimum stable rates.
This can result in optimistic predictions for minimum stable flow rates.
Hagedorn Brown should not be used for condensates and whenever mist flow is the main flow regime.

Note: In Prosper software, the deviation correction for holdup of Duns & Ros has been added to the Hagedorn & Brown correlation

Beggs & Brill (Std.):

The Beggs & Brill correlation was developed following a study of two-phase flow in horizontal and inclined 1 inch and 1 ½ inch smooth circular pipes. It is primarily a pipeline correlation and generally over-predicts pressure drops in vertical and deviated wells.
The correlation is based upon a flow regime map, which is first determined, as if the flow was horizontal. A horizontal holdup is then calculated by correlations, and this holdup is corrected for the angle of inclination.

Beggs and Brill (no-slip):

It uses the same methodology as the standard Beggs and Brill, with the exception that the holdup used is not the horizontal holdup described above, but simply the no-slip holdup, without deviation correction.

Beggs and Brill (modified):

It also uses the same methodology as the standard Beggs and Brill, with the following changes:

There is no extra flow regime of froth flow, which (as in Duns and Ros (modified)) assumes a no-slip holdup.
The friction factor is changed from the smooth pipe model to the method used in Duns and Ros (modified) – a single-phase friction factor using pipe roughness and average fluid velocity.

Note: In Pipesim software, it’s called Beggs and Brill Revised, but with extra flow regime of froth flow.

Petroleum Expert:

The Petroleum Experts correlation combines the best features of existing correlations. It uses the Gould et al flow map and the Hagedorn Brown correlation in slug flow, and Duns and Ros for mist flow. In the transition regime, a combination of slug and mist results is used.

Petroleum Expert 2:

The Petroleum Experts 2 correlation has improved VLP calculations for low rates and well stability. It provides more accurate prediction of minimum load-up rates.

Petroleum Expert 3:

The Petroleum Experts 3 includes the features of the PE2 correlation plus original work for viscous, volatile and foamy oils.

Petroleum Expert 4:

The Petroleum Experts 4 is an advanced mechanistic model suitable for any angled wells (including downhill flow) suitable for any fluid (including Retrograde Condensate). It is especially good correlation for pipeline pressure drop calculations and instability calculations (detecting the conditions at which instability will occur).

Petroleum Expert 5:

The Petroleum Experts 5 mechanistic correlation is an advancement on the PE4 mechanistic correlation. PE4 showed some instabilities (just like other mechanistic models) that limited its use across the board. PE5 reduces the instabilities through a calculation that does not use flow regime maps as a starting point.

PE5 is capable of modeling any fluid type over any well or pipe trajectory. This correlation accounts for fluid density changes for incline and decline trajectories.

The stability of the well can also be verified with the use of PE5 when calculating the gradient traverse, allowing for liquid loading, slug frequency, etc. to be modeled.

Orkiszewski:

Orkiszewski developed a pressure drop prediction method based on a new flow pattern map and a combination of features from existing correlations. He combined the work of Griffith for bubble flow and that of Griffith and Wallis for slug flow together with the Duns and Ros correlation for mist flow. In addition, new friction and density correlations for slug flow based on a liquid distribution parameter were developed. The data of Hagedorn was used to develop a correlation with tubing size, superficial mixture velocity, and liquid viscosity.

Orkiszewski correlation often gives a good match to measured data. However, its formulation includes a discontinuity in its calculation method. The discontinuity can cause instability during the pressure matching process. Therefore, the use of Orkiszewski is discouraged due to the danger of encountering a pressure discontinuity during pressure matching and VLP calculations.

Mukherjee & Brill:

The Mukherjee & Brill correlation was developed following a study of pressure drop behavior in a two-phase inclined flow.

For bubble and slug flow, a no-slip friction factor calculated from the Moody diagram was found adequate for friction head loss calculations.
In downhill-stratified flow, the friction pressure gradient is calculated based on a momentum balance equation for either phase assuming a smooth gas-liquid interface.
For annular – mist flow, a friction factor correlation was presented that is a function of holdup ratio and no-slip Moody friction factor.
Results agreed well with the experimental data and correlations were further verified with Prudhoe Bayand North Sea data.

Aziz, et al.:

Aziz et al developed a mechanistically based model and concentrated their research on the bubble and slug flow regimes. Predictions for 48 wells were compared to field data and with the predictions from Orkiszewski, Duns and Ros and Hagedorn and Brown. Also, they revised the flow regime map.

Ansari:

The Ansari model was developed as part of the Tulsa University Fluid Flow Projects (TUFFP) research program.
A comprehensive model was formulated to predict flow patterns and the flow characteristics of the predicted flow patterns for upward two-phase flow.
The comprehensive mechanistic model is composed of a model for flow pattern prediction and a set of independent models for predicting holdup and pressure drop in bubble, slug, and annular flows.
The model was evaluated by using the TUFFP well databank that is composed of 1775 well cases, with 371 of them from Prudhoe Bay data.

Gray:

Gray correlation gives good results in gas wells for condensate ratios up to around 50 bbl/MMscf and high produced water ratios. Gray correlation contains its own internal PVT model which over-rides PROSPER’s normal PVT calculations. For very high liquid dropout wells, use a Retrograde Condensate PVT and the Duns and Ros correlation.