Pressure and depth:
“Pressure and Depth” is the FUNDAMENTAL relationship in the oil industry. Your understanding of the concept is crucial. The easiest way to calculate pressure from depth is to use the pressure gradient of the given fluid.
Pressure gradients for incompressible fluids have units of pressure/depth. For example, psi/ft, bar/m.
Pressure gradient seems difficult, but it is simply using the density of the fluid and converting units:
The density of pure water is 1000 kg/m3. To convert to gradient:
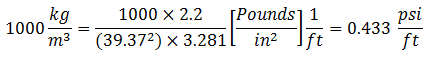
- 1 kg = 2.2 pounds
- 1 m = 39.37 inches
- 1 m = 3.28 feet
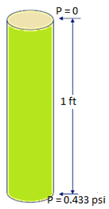
0.433 is the gradient for pure water (SG = 1) in Imperial units, remember it.
NB: Specific Gravity is always relative to pure water.
Calculating Pressure Gradient:
Most of the time you will not be given a fluid gradient or an average specific gravity, you will need to calculate it.
First calculate your average specific gravity:
Average SG = SG of water x Water Cut + SG of oil x (1-Water Cut)
Then calculate your Gradient:
Average Gradient = 0.433 x Average SG
If you are given the API gravity of oil instead of the SG, then use this formula:
Example:
WC = 70%
Water SG = 1.04
Oil Gravity = 36 °API
Calculate the average Gradient:
- Oil density = 141.5 / (131.5 + 36) = 0.845
- Average density = 1.04×0.7 + 0.845×0.3 = 0.9815
- Average Gradient = 0.433 x 0.9815 = 0.425 psi/ft.
Pressure-Depth Plot:
To find a pressure at a given depth, simply multiply the VERTICAL depth by the given fluid gradient.
Pressure = Density x Gradient
Assuming that the fluid is incompressible, this is a linear relationship.
We can draw this on a graph that we call the pressure-depth plot.
Obviously, denser fluids, and therefore higher fluid gradients result in higher pressure.
For example, if my depth is 2000 ft. and my gradient is 0.425 psi/ft, then my pressure is 2000 ft. x 0.425psi/ft = 850 psi.
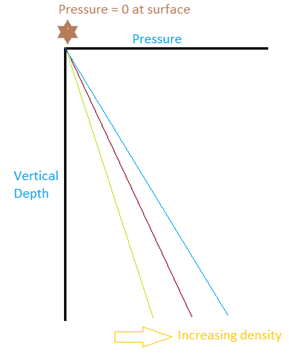
If the pressure at surface isn’t zero, then the whole line shifts over according to the surface pressure.
Example:
From the previous example, a gradient of 0.425 psi/ft at 2000 ft. resulted in 850 psi pressure.
If my surface pressure was 150 psi, then the pressure at depth would increase by the same amount:
Pressure @ depth = 850 psi + 150 psi = 1000 psi.
If the fluid doesn’t reach the surface, then there is some ‘fluid level’, or depth, where the pressure is zero and then the pressure increases according to the gradient.
Example:
Our total depth (2000 ft.) and gradient (0.425 psi/ft.) are the same as before. The fluid level, however, is below the surface (zero) at 500 ft. What is the pressure at 2000 ft.?
P = (2000 ft. – 500 ft.) x (0.425 psi/ft.) = 637.5 psi.
Calculating the Fluid Height or Column:
Similarly, if we know the pressure and the gradient, we can calculate the equivalent fluid column resulting from that pressure.
Fluid Height = Pressure / Gradient
Here the effect of increasing gradient is reversed, and denser fluid results in a shorter fluid column for a given pressure.
Example:
Pressure = 2500 psi @ depth (pressure zero at surface).
Gradient = 0.402 psi/ft.
Fluid Height = (2500 psi.) / (0.402-psi/ft.) = 6218.9 ft.
You May Also Like…
- Well Inflow Performance
- Introduction to IPR and VLP
- Vogel’s inflow performance relationship
- The Composite Inflow Performance Relationship
- Pressure drawdown & Skin Factor
- Multiphase flow regimes
- Multiphase Flow Properties & Pressure Gradient Calculation
- Multiphase flow correlations
